Kolumne

oder: Warum Sie in der Dunkelkammer in Blendenschritten denken sollten

Thomas Wollstein
Feb. 2001

Eine Warnung am Anfang: Dieser Artikel ist für die mathematisch vorgebildeten Profis wahrscheinlich langweilig. Für die habe ich ihn auch nicht geschrieben. Vielmehr geht es mir um diejenigen Fotografen, die schon bei dem Gedanken an Mathematik Pickel bekommen.

Niemand würde auf den Gedanken kommen, mit der Kamera eine Belichtungsreihe mit den Schritten 1/125, 1/250, 1/375, 1/500, 1/675 Sekunde usw. aufzunehmen, sondern man benutzt folgerichtig Schritte, bei denen zwischen einer Aufnahme und der nächsten nicht eine konstante Schrittweite, sondern ein konstanter Faktor liegt, z. B. ein Faktor 2, der gerade einem ganzen Blendenschritt entspricht. Das mag an den eingeschränkten Einstellmöglichkeiten der Kameras liegen, die uns die krummen Werte mit konstanter Schrittweite gar nicht anbieten (aber diese Einschränkung hat ihren Sinn).

Soweit zur Situation bei der Aufnahme. Wenn man jetzt in die Dunkelkammer geht, um ein aufgenommenes Foto zu vergrößern, wird man nicht mehr durch die Einstellungsmöglichkeiten der Kamera eingeschränkt. Als Konsequenz werden immer wieder Probestreifen mit z. B. 2 / 4 / 6 / 8 / 10 Sekunden usw. angefertigt, weil's ja so einfach ist. Dabei macht das wenig Sinn. Genau wie der Film "denkt" das Fotopapier logarithmisch. Im Klartext heißt das, dass die Schwärzung eines Fotopapiers bei einer Verdopplung der Belichtung um denselben Betrag zunimmt, gleich ob man von 10 auf 20 Sekunden oder von 40 auf 80 Sekunden verdoppelt. (Das gilt ganz streng nur in einem bestimmten - dem linearen - Bereich von Belichtungen, mehr dazu weiter unten.)

Die konsequente Umsetzung dieser Idee findet man in solchen Laborschaltuhren und -messgeräten, die einem Änderungen der eingestellten Belichtungszeiten in Blendenschritten anbieten. Ein solches Gerät kann einem die Kopfrechnerei abnehmen, aber laufen Sie jetzt nicht gleich in den Laden, um eins zu kaufen. Ein bisschen Kopfrechnen oder ein primitiver Taschenrechner tun's auch.

Was passiert denn bei einem Probestreifen, der mit konstanter Schrittweite (also z. B. immer 2 s) belichtet wurde? Ganz einfach: Der Schwärzungsunterschied von einer Probe zur nächsten nimmt immer weiter ab. Gehen wir davon aus, dass alle genannten Belichtungen im linearen Bereich liegen. Während z. B. bei der oben genannten Reihe der Schritt von 2 nach 4 s noch eine Blende beträgt und deutlich sichtbar sein sollte, beträgt der Schritt von 4 nach 6 s nur noch mehr als eine halbe Blende (nein, nicht genau eine halbe Blende, wegen des Logarithmus, s. u.). Entsprechend nimmt die Schwärzung um einen deutlich geringeren Betrag zu. Von 6 nach 8 s ist der Belichtungsunterschied schon nur noch knapp eine halbe Blende, und mit jedem weiteren Schritt auf der Leiter nimmt er - und mit ihm der entsprechende Dichtezuwachs - ab. Beträgt der Belichtungsunterschied von einer Probe zur nächsten weniger als ¼ Blende, wird er manchmal schon schwierig zu sehen sein.

Anders bei Belichtungsänderungen um einen konstanten Faktor: Wenn Sie einen Probestreifen mit 2, 4, 8, 16, 32 s anfertigen, beträgt der Schritt von einer Probe zur nächsten immer eine ganze Blende, entsprechend wird der Dichtezuwachs immer gleich sein (unter der o. g. Voraussetzung, Stichwort Linearität). Sie haben auf diese Weise mit 5 Probebelichtungen den Bereich von 2 bis 32 s abgedeckt, während sie bei der Methode mit konstanter Schrittweite nur von 2 bis 10 s gekommen sind.

Nun ist aber ein ganzer Blendenschritt von einer Probebelichtung zur nächsten i. d. R. doch ein bisschen zuviel, zumindest für eine genaue Bestimmung der optimalen Belichtungszeit. Für das grobe Eingrenzen, wenn man gar nichts weiß, sind ganze Blendenschritte aber gut geeignet. Was tun bei halben oder viertel Blendenschritten?

Nun, viel muss man sich nicht merken: 1 Blendenschritt entspricht einem Faktor von 2, ½ Blendenschritt 1,4 (genau Wurzel aus 2, aber die Nachkommastellen bringen uns nicht um), ¼ Blendenschritt 1,2. Also wäre eine geeignete Reihe von Probebelichtungen in halben Blendenschritten z. B. die folgende:

2 / 2,8 / 4 / 5,6 / 8 / 11 / 16 / 22 / 32 / 45 / 64 s

Jetzt schreien bestimmt einige auf:

Diese Zahlenreihe kommt einem doch verdammt bekannt vor, nicht wahr? Richtig: das sind die Werte der genormten internationalen Blendenreihe. (Die Werte sind etwas gerundet. Die genauen Werte weichen aber nur unbedeutend von den gerundeten ab, und die gerundeten sind leichter zu behalten.)

Um das Merken und Kopfrechnen weiter zu erleichtern, möchte ich noch auf etwas hinweisen (das auch an dem konstanten Faktor liegt): Mit der krummen Zahl 1,4 müssen Sie nur am Anfang Ihren Startwert (hier: 2 s) multiplizieren. Alle folgenden Werte ergeben sich jeweils durch Verdopplung des vorletzten Wertes, also der dritte Wert aus dem ersten, der vierte aus dem zweiten, der fünfte aus dem dritten ...

Zurück zur Anwendung: Belichtungszugabe um einen bestimmten Faktor entspricht Multiplikation mit dem Faktor, knappere Belichtung Division durch den Faktor, konkret

Die Tabelle können Sie sich in der Duka an die Wand pinnen und einen Taschenrechner mitnehmen, wenn Sie keine Luxus-Schaltuhr haben. Wenn Sie dem Kopfrechnen nicht zu ablehnend gegenüber stehen, merken Sie sich nur die folgende abgespeckte Tabelle in Prozentschritten.

Dass die Werte nach unten und oben nicht symmetrisch sind (dass also eine halbe Blende weniger 30 % Abzug sind, eine halbe Blende mehr aber 40 % Zugabe), liegt - man ahnt es schon - am Logarithmus. Unter uns gesagt: Sie machen auch keinen gar zu großen Fehler, wenn Sie sich nur die 20 und 40 % merken. Immer noch besser als die konstante Schrittweite!

Warum der ganze Eiertanz?

Sie kommen doch mit den konstanten Schrittweiten irgendwann auch zur optimalen Belichtungszeit.

Die Antwort liegt zum einem in dem "irgendwann" im vorangehenden Satz. Wie oben dargestellt, decken Sie mit Belichtungsreihen in Blendenschritten (ganzen oder Bruchteilen) mit derselben Anzahl von Probebelichtungen einen größeren Bereich ab. Sie brauchen also weniger Versuche, um die "richtige" Zeit zu finden, mithin weniger Material und weniger Zeit.
Aber auch das ist nicht der eigentliche Grund, warum mir die Blendenschritte so am Herzen liegen: Wie schon gesagt, orientieren sich die Blendenschritte am Verhalten des Fotomaterials und nicht an unserer Bequemlichkeit. Wenn Sie sich dazu durchringen, in der Dunkelkammer in Blendenschritten zu denken, werden Sie bald eine erwünschte Nebenwirkung (ganz ohne Risiko) bemerken.

Stellen Sie sich folgende Situation vor: Sie haben einen Probestreifen gemacht und kamen zu dem Schluss, die "richtige" Belichtungszeit sei 15 s. Jetzt fertigen Sie eine Vergrößerung mit dieser Zeit an, und nach dem Trocknen stellen Sie fest, dass sie Ihnen doch etwas zu dunkel ausgefallen ist. (Vielleicht haben Sie den Probestreifen nass beurteilt und den Dry-Down-Effekt vergessen.) Sie entschließen sich, um eine Viertel Blende knapper zu belichten, also z. B.

15 s ÷ 1,2 = 12,5 s

Wenn Sie solche Änderungen nach oben und unten ein paarmal gemacht haben, bekommen Sie ein prima Gefühl dafür, welche Änderungen der Belichtung welche Auswirkungen auf Ihr Bild haben. Es ist viel schwieriger, dieses Gefühl zu bekommen, wenn Sie Belichtungsänderungen immer als absolute Werte und nicht im Verhältnis zum Ausgangswert betrachten. Das ist die eigentliche Motivation für die ganze lange Erklärung.

Wenn Sie aus der Schule nur ungute Erinnerungen an den Logarithmus haben und das auch nicht ändern wollen, hören Sie hier besser auf zu lesen. Wenn Sie aber vielleicht im Hinblick auf Ihr Hobby doch etwas daran ändern wollen und ein ganz kleines bisschen über das Verhalten von Fotopapieren lernen wollen, lesen Sie weiter.
Was ist der "lineare Bereich"?

Dazu zeige ich Ihnen eine Schwärzungskurve, die ich mit "Hausmitteln" selbst gemessen habe. Sie entstand, indem ich einen Durchsichtsgraukeil im Kontakt auf ein Blatt Fotopapier kopiert habe und die Schwärzung mithilfe eines Scanners ausgewertet habe. Die Kurve ist damit qualitativ sicher nicht mit solchen zu vergleichen, die mit einem hochwertigen Reflexionsdensitometer bestimmt wurden, aber für meine Zwecke reicht es allemal.

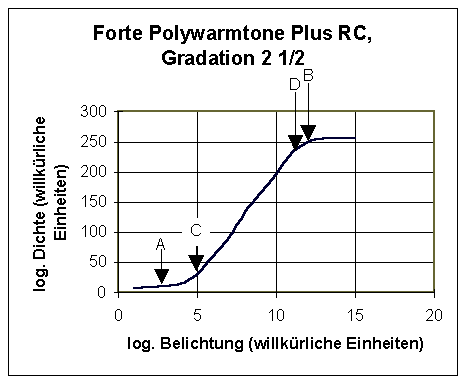
Sie sehen Folgendes:

• Eine Belichtung des Fotopapiers unterhalb einer Schwelle (A), hier etwa beim Wert 4 auf der Belichtungsachse, bewirkt keine sichtbare Schwärzung.
• Eine Belichtung über einen bestimmten Wert hinaus, hier etwa 12 (B) bewirkt keine Zunahme der Schwärzung mehr. (Klar: Wenn alles Bildsilber belichtet ist, ist das Papier nach dem Entwickeln so schwarz wie es eben werden kann. Mehr geht auch mit mehr Licht nicht.)
• Zwischen diesen beiden Extremem erstreckt sich von C bis D der so genannte "lineare Bereich". Zwischen etwa 5 und etwa 12 Belichtungseinheiten gelten die oben beschriebenen Zusammenhänge, d. h. wenn ich von 6 nach 7 auf der Belichtungsachse gehe, nimmt die Schwärzung um näherungsweise 40 Einheiten zu, wenn ich von 10 nach 11 gehe auch, und auch bei jedem entsprechenden Schritt dazwischen.

Jetzt höre ich Sie rufen: Eben hat er uns etwas von Faktoren erzählt, und jetzt redet er doch wieder von Schrittweiten! Beachten Sie aber, dass die Belichtungseinheiten logarithmisch sind. "5" ist nicht die Belichtungszeit, sondern ihr Logarithmus! Wenn ich zwei logarithmische Werte addiere, kommt wieder ein logarithmischer Wert heraus, und zwar derselbe, den ich erhalten würde, wenn ich die beiden nicht logarithmischen Werte mit einander multiplizieren würde und erst dann den Logarithmus bilden würde. Zu abstrakt? Also gut, ein Zahlenbeispiel:

Mit dieser Erklärung habe ich dann auch gleich den zweiten offenen Punkt abgehakt, nämlich die Frage, wie der Logarithmus in die Überschrift kam.

Bleibt der Vollständigkeit halber noch eine Einschränkung der Linearität nachzureichen: Sie ergibt sich durch den so genannten Reziprozitätsfehler, für den alle Fotomaterialien anfällig sind: Nur im Bereich "vernünftiger" Zeiten gilt, dass eine Belichtung von z. B. 10 s bei Blende 5,6 dieselbe Schwärzung ergibt wie 20 s bei Blende 8. Was "vernünftig" im Einzelfall bedeutet, hängt von der Anwendung ab: Bei Film wären schon 10 s nicht "vernünftig", und Sie müssten vermutlich erheblich länger als 20 s belichten, um bei Schließen der Blende um eine Stufe dieselbe Schwärzung zu erzielen. Aber bei Papier setzt der Reziprozitätsfehler, oft auch Schwarzschildeffekt genannt, erst bei ganz anderen Zeiten ein, nämlich i. d. R. bei so langen, dass er bei üblichen Vergrößerungsmaßstäben und Lichtquellen keine große Rolle spielt.