Bitte ein Bit (und noch eins und noch eins und noch eins ...)
Warum es besser ist, Bilder mit mehr Bits zu scannen
Thomas Wollstein
Mai 2003
Meine Scanner-Treiber bieten mir an, die Daten meiner farbigen Vorlagen oder Negative mit 24, 36, 42 oder gar 48 bit je Kanal an Bildbearbeitungssoftware weiterzureichen, aber mein Drucker kann nur mit 24-bit-Farbdaten etwas anfangen. Und mein Drucker ist da nicht allein: M.W. gibt es kein einziges Ausgabegerät, dass Daten mit mehr als 8 bit je Kanal (24 bit bei RGB-Farbdateien) unterstützt. Auch viele Bildbearbeitungsprogramme unterstützen nur Daten mit 8 bit je Kanal, und die, die bis zu 16 bit vertragen (z. B. Photoshop), stellen in diesem Modus nicht alle Funktionen zur Verfügung. So funktionieren zwar die globalen Tonwertanpassungen und bestimmte Pinselfunktionen, aber z. B. nicht ein einziges Filter. Stellt sich also die Frage:
Wozu sind die vielen Bits gut?
Grundlegendes
Aufgabe des Scanners ist es, die kontinuierlichen Tonwerte einer Vorlage in diskrete digitale Daten umzuwandeln. "Kontinuierlich" bedeutet folgendes: Wenn ich einen Tonwert X habe, dann kann in der Vorlage auch ein beliebig geringfügig von diesem verschiedener Tonwert X+Δ vorkommen. Digitale Werte aber sind diskret. Das bedeutet, wenn Tonwert X digital z. B. als Zahl 5 dargestellt wird, dann muss sich die Software überlegen, ob sie den ganz leicht von X verschiedenen Wert X+Δ auch als 5 oder schon als 6 darstellen soll. Wird aber der Wert X+Δ nicht als vom Wert X verschieden erkannt, geht Information verloren, das Bild wird "schlechter".
Wie groß der Wert Δ ist, um den sich zwei Tonwerte der Vorlage unterscheiden müssen, damit sie in der Datei als verschieden gespeichert werden, hängt bei einer gegebenen Vorlage davon ab, wie viele Werte zur Verfügung stehen, um den Vorlagenumfang in Zahlen umzusetzen. Bietet uns die Software 8 bit an, so heißt das, dass der Vorlagenumfang in Werte von 0 bis 255, also 256 Abstufungen umgesetzt werden kann. Bietet sie mehr Bits an, können die vorhandenen Tonwerte auf mehr Zahlen verteilt werden, was bedeutet, dass kleinere Unterschiede in der Vorlage auch als kleinere Unterschiede in der Datei sichtbar werden, dass also beim Scannen weniger Information verloren geht.
Üblicherweise geht man davon aus, dass 8 bit ausreichen, um Grauschattierungen zu erzeugen, die feiner sind als das, was das menschliche Auge noch unterscheiden kann. Dann entsteht der Eindruck eines kontinuierlichen Tonwertverlaufs. Daher auch die Beschränkung der Ausgabegeräte auf diese Bit-Tiefe.
Bei Farbvorlagen braucht man die 8 bit für jede der drei Grundfarben, die zugehörigen Dateien haben also 24 bit je Pixel. Ich werde im Folgenden also von 8/24- und 16/48-bit-Dateien reden und damit meinen, dass mit 8 bzw. 16 bit je Kanal (Grau oder RGB) und daher mit 24 bzw. 48 bit je Pixel gearbeitet wird. Andere Bit-Tiefen sind möglich (s.o.), aber vom Grundsatz her gilt dieselbe Argumentation, so dass ich nur über die Extremwerte reden werde.
Erklären möchte ich Ihnen im Folgenden, warum es sinnvoll ist, mit hohen Bitzahlen zu scannen und teilweise auch zu arbeiten, obwohl Ihr Drucker doch nur ein 8/24-bit-Ausgabegerät ist.
Offenkundige Vorteile von 16/48-bit-Dateien
Nach dem Vorstehenden ist klar, dass 16/48-bit-Dateien mehr nützliche Bildinformation enthalten.
Offenkundige Nachteile von 16/48-bit-Dateien
- 16/48-bit-Dateien benötigen doppelt so viel Platz auf Ihrer Festplatte und im Hauptspeicher Ihres Rechners.
- Software unterstützt 16/48-bit-Dateien gar nicht oder nur eingeschränkt.
Nicht gleich ersichtliche Vorteile von 16/48-bit-Dateien
Stellen wir uns vor, wir müssten den Bereich der Zahlen von 0 (Weiß) bis 1 (Schwarz) mit 10 Zahlen wiedergeben. Dann würden wir vielleicht folgende Zuordnung treffen:
Vorlagenwert wird dargestellt als Zahlenwert
|
Vorlagenwert |
wird dargestellt als |
Zahlenwert |
|
0 bis 0,1 |
-> |
0 |
|
0,1 bis 0,2 |
-> |
1 |
|
usw. bis |
|
|
|
0,9 bis 1 |
-> |
9 |
Von einer Vorlage, in der alle Werte zwischen Weiß und Schwarz vorkommen (Davon gehen wir im Folgenden immer aus.), erzeugen wir also zunächst eine Datei mit den Werten 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Jetzt passen wir den Kontrast der Datei an, weil uns ein bestimmter Tonwertebereich besonders wichtig ist. Nehmen wir an, wir wollten den Kontrast um den Faktor 1,5 steigern, dann würden zunächst rein rechnerisch aus den vorhandenen Werten
|
alter Wert |
x 1,5 wird rechnerisch |
übrig bleibt aber nur der neue Wert |
|
0 |
0 |
0 |
|
1 |
1,5 |
2 |
|
2 |
3 |
3 |
|
3 |
4,5 |
5 |
|
4 |
6 |
6 |
|
5 |
7,5 |
8 |
|
6 |
9 |
9 |
|
7 |
10,5 |
9 |
|
8 |
12 |
9 |
|
9 |
13,5 |
9 |
Da uns nur die Werte von 0 bis 9 zur Verfügung standen, geht zunächst einmal alle Information verloren, die oberhalb von Tonwert 6 lag.
Anmerkung: Wenn man den Mittelbereich expandiert hätte, gäbe es Verluste in den niedrigen und hohen Werten, wenn man die hohen Werte expandiert hätte, bei den niedrigen Werten. Die Argumentation ist überall dieselbe, so dass ich mich hier auf einen Fall beschränke.
Das ist aber nur ein Teil der Wahrheit: Wenn Sie sich jetzt einmal ansehen, welche Werte überhaupt noch auftauchen (rechte Spalte), werden Sie bemerken, dass nur noch 0, 2, 3, 5, 6, 8 und 9 vorkommen, d.h. statt der vorher vorhandenen 10 Tonwerte nur noch 7! Die Tonwerte 1, 4 und 7 kommen nicht mehr vor.
Wiederholen wir die Übung, stellen jedoch diesmal die vorhandenen Werte von 0 bis 1 als Zahlen von 0 bis 19 dar, also durch 20 Werte
|
Vorlagenwert |
wird dargestellt als |
Zahlenwert |
|
0 bis 0,05 |
-> |
0 |
|
0,05 bis 0,1 |
-> |
1 |
|
0,1 bis 0,15 |
-> |
2 |
|
usw. bis |
|
|
|
0,95 bis 1 |
-> |
19 |
und spielen wir wieder dasselbe Spiel, also die Kontrastanpassung x 1,5. Folgendes passiert nun:
|
alter Wert |
x 1,5 wird rechnerisch |
übrig bleibt aber nur der neue Wert |
|
0 |
0 |
0 |
|
1 |
1,5 |
2 |
|
2 |
3 |
3 |
|
3 |
4,5 |
5 |
|
4 |
6 |
6 |
|
5 |
7,5 |
8 |
|
6 |
9 |
9 |
|
7 |
10,5 |
11 |
|
8 |
12 |
12 |
|
9 |
13,5 |
14 |
|
10 |
15 |
15 |
|
11 |
16,5 |
17 |
|
12 |
18 |
18 |
|
13 |
19,5 |
19 |
|
14 |
21 |
19 |
|
15 |
22,5 |
19 |
|
16 |
24 |
19 |
|
17 |
25,5 |
19 |
|
18 |
27 |
19 |
|
19 |
28,5 |
19 |
Der Informationsverlust in den Werten ab 13 tritt auf wie bei der Darstellung mit 10 Zahlen, und auch in den unteren Werten kommen wieder ein paar Werte nicht vor. Also kein Gewinn?
Doch! Denn wenn wir jetzt die Darstellung durch 20 Zahlen auf eine mit 10 Zahlen herunterrechnen, wie wir es tun, wenn wir eine 16/48-bit-Datei zum Drucker schicken, bietet sich ein interessantes Bild: In der folgenden Tabelle sind in der linken Spalte die Werte, die in unserem Beispiel nach der Kontrastanpassung nicht mehr vorkommen, rot markiert. Wir müssen zum Herunterrechnen immer zwei benachbarte Werte zu einem zusammenfassen
|
alter Wert |
wird heruntergerechnet |
zu |
|
0 |
} |
0 |
|
1 |
||
|
2 |
} |
1 |
|
3 |
||
|
4 |
} |
2 |
|
5 |
||
|
6 |
} |
3 |
|
7 |
||
|
8 |
} |
4 |
|
9 |
||
|
10 |
} |
5 |
|
11 |
||
|
12 |
} |
6 |
|
13 |
||
|
14 |
} |
7 |
|
15 |
||
|
16 |
} |
8 |
|
17 |
||
|
18 |
} |
9 |
|
19 |
Wenn wir also zunächst mit vielen, fein abgestuften Werten arbeiten, dann den Kontrast anpassen und schließlich wieder auf die grobe Darstellung herunterrechnen, bekommen wir eine Darstellung, in der alleWerte vorhanden sind, also keine Löcher in der Skala auftreten.
Allerdings tritt eine andere Nebenwirkung auf: In der rechten Spalte des letzten Beispiels sind diejenigen Werte der am Ende resultierenden Darstellung blau markiert, bei denen bei der Zusammenfassung mehrere Werte auf einen Zielwert zusammengezogen wurden. Manche Werte werden also durch die Anpassung gegenüber den anderen bevorzugt, mit anderen Worten, überbewertet.
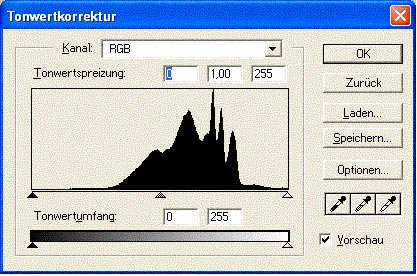
Was wir hier mit Zahlen zu Fuß gemacht haben, sieht man in Bildbearbeitungsprogrammen als Histogramm. Fehlende Tonwerte zeigen sich im Histogramm als Löcher, die überbewerteten Werte als so genannte Spikes, Nadelspitzen, die sich auffallend über die benachbarten Werte erheben.
Beispiele bieten die beiden nachfolgenden Histogramme: Bild 1 zeigt das Histogramm eines unbearbeiteten Bildes, wie es bei einer Aufnahme unter recht kontrastarmen Bedingungen im Automatikmodus von meiner Nikon Coolpix erzeugt wurde.
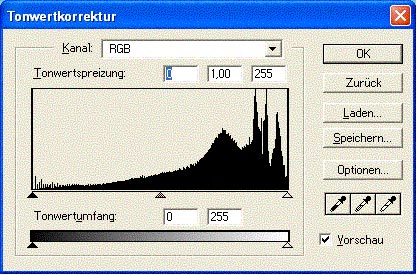
Es liegt nahe, die Tonwerte dieses Bildes auseinanderzuziehen, um die gesamte Skala zu füllen. So entstand das Histogramm in Bild 2. Hier sind im Bereich der Schatten ganz kleine Löcher und Spitzen zu erkennen, die allerdings noch nicht zu im Ausdruck sichtbaren Problemen führten.
Löcher im Histogramm sind nicht automatisch ein Problem, zumal nicht, wenn sie nur bei einzelnen Tonwerten und nicht gehäuft in einem Tonwertbereich (Schatten, Mitteltöne oder Lichter) auftreten. Nehmen wir z. B. an, unser Auge könnte in der Größenordnung von 100 Tonwerten zwischen Schwarz und Weiß auflösen, und wir haben für die Darstellung 200 Tonwerte genutzt, dann würde es nicht einmal auffallen, wenn bei jedem zweiten Tonwert ein Loch im Histogramm wäre. Wenn aber an einer Stelle mindestens zwei benachbarte Tonwerte fehlen, dann kann das einen erkennbaren Sprung bedeuten.
Ob dieser Sprung tatsächlich erkennbar wird, hängt vom Bild ab. Ein Foto, bei dem keine flächigen Tonwertverläufe auftreten, ist i. Allg. weniger gefährdet, da dort von einem Pixel zum nächsten meist größere Sprünge auftreten, in denen der fehlende Tonwert "untergeht". Die beiden möglicherweise auftretenden Effekte heißen auf Neudeutsch Posterization und Banding, in Deutsch Farbsprünge und Farbbänder.
Als Posterization (oder Farbsprung) wird es bezeichnet, wenn ein an sich kontinuierlicher Tonwertübergang im Bild als ein abrupter, stufiger Übergang erkennbar wird.
(Beispiel: http://www.michaeldvd.com.au/Articles/VideoArtefacts/VideoArtefactsPosterization.html)
Banding (bzw. die Bildung von Farbbändern) wird besonders dann ein Problem, wenn im Bild großflächige Tonwertverläufe auftreten. Haben Sie z. B. einen Sonnenuntergang fotografiert, so klingt die Helligkeit vom Bild der Sonne her nach außen kontinuierlich ab. Banding führt dazu, dass kein kontinuierlicher Verlauf zustande kommt, sondern sich jeweils in sich einfarbige Ringe um die Sonne bilden, zwischen denen jedoch von einem zum nächsten abrupte Übergänge auftreten. Im Prinzip ist es dasselbe wie Posterization, nur wegen der Großflächigkeit noch störender.
|
|
Bild 3 zeigt den Effekt im Bereich des Himmels. |
Folgerungen
Schlussfolgerungen aus dem zuvor Gesagten sind folgende:
- Scannen Sie Vorlagen und Negative zunächst mit der größtmöglichen Bit-Tiefe, die Ihnen Ihr Treiber anbietet und die Ihre Bildbearbeitungssoftware verarbeiten kann.
- Führen Sie globale Tonwert- und Farbanpassungen mit den fein aufgelösten Daten durch.
- Ändern Sie dann erst den Modus auf 8/24-bit-Darstellung und führen die noch verbleibenden Änderungen durch.
Tonwertanpassung in der Scanner-Software oder Digitalkamera oder in der Bildbearbeitungssoftware?
Nicht nur die Bildbearbeitungssoftware, sondern auch Scannertreiber und hochwertige Digitalkameras bieten die Möglichkeit, globale Tonwertanpassungen durchzuführen. Wo sollte man zuschlagen?
I. Allg. ist es sinnvoll, möglichst viele Anpassungen schon auf der ersten Stufe, also Scanner/Kamera durchzuführen. Das gilt insbesondere dann, wenn Sie Bildbearbeitungssoftware nutzen, die nur 8/24-bit-Daten verkraftet. Die Treibersoftware für Scanner/Kamera passt nämlich die "hochbittigen" Daten an und überträgt dann erst die 8/24-bit-Daten.
Verfügen Sie über Software, die 16/48-bit-Daten verarbeitet, ist es i. Allg. günstiger, in der Bildbearbeitungssoftware zu ändern, da Sie dort den großen Bildschirm Ihres Rechners und nicht nur den briefmarkengroßen Vorschau-Bildschirm der Scannersoftware oder Kamera nutzen können. In diesem Fall würde ich Ihnen also raten, nur die allergröbsten Anpassungen über Scanner/Kamera vorzunehmen, aber die Feinarbeit in der Bildbearbeitungssoftware zu erledigen.


